Cartographier un territoire implique de pouvoir localiser des points géographiques sur une surface plane avec un système de coordonnées euclidien en (x, y). En effet, les cartes planes s’avèrent beaucoup plus utiles que des globes dans biens des situations: elles sont plus faciles à produire et à transporter et on peut les visualiser sur des écrans à différentes échelles. Ce processus de projection dans le plan implique deux étapes:

Étape 1 - La terre est ronde, ou presque

Le globe terrestre n’est pas parfaitement sphérique. Sa forme réelle est celle d’un patatoïde (géoïde) qui présente des irrégularités: renflements au niveau des zones montagneuses, dépressions au niveau des océans. Un point à la surface de la Terre est donc représenté dans un système de coordonnées sphérique à trois dimensions (latitude, longitude, altitude). La première étape consiste à s’affranchir de l’altitude en approximant la forme du géoïde par un ellipsoïde de révolution.

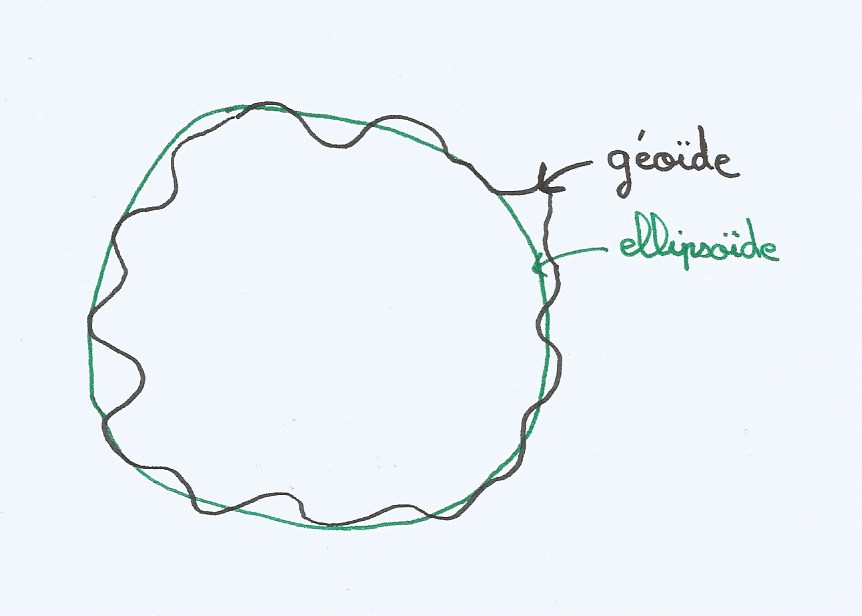
Il devient alors possible de positionner un point à la surface de la Terre avec seulement deux coordonnées (latitude, longitude), l’altitude se déduisant des deux autres. L’ellipsoïde la plus connue est le World Geodetic System WGS84. C’est le standard utilisé par le système GPS. D’autres standards existent qui permettent des ajustements locaux avec des ellipsoïdes dont le centre ne correspond pas nécessairement avec le centre de gravité de la Terre.

Calculer des distances entre des points à la surface de l’ellipsoïde est une tâche relativement complexe. Il existe des librairies permettant de le faire comme geopy À noter que la distance entre deux points dépend de l’ellipsoïde choisie:

Étape 2 - Mettre à plat

La deuxième étape consiste dérouler la surface de l’ellipsoïde dans le plan. D’un point de vue mathématiques, une projection permet d’établir une correspondance telle que:

$$x = f1(\alpha, \lambda) $$ $$ y = f2(\alpha, \lambda)$$

où \(x, y\) désignent les coordonnées planes, \(\alpha\) la latitude, \(\lambda \) la longitude et \(f1, f2\) des fonctions qui sont continues partout sur l'ensemble de départ sauf sur un petit nombre de lignes et de points (tels que les pôles). Il existe une infinités de solutions à cette équation.

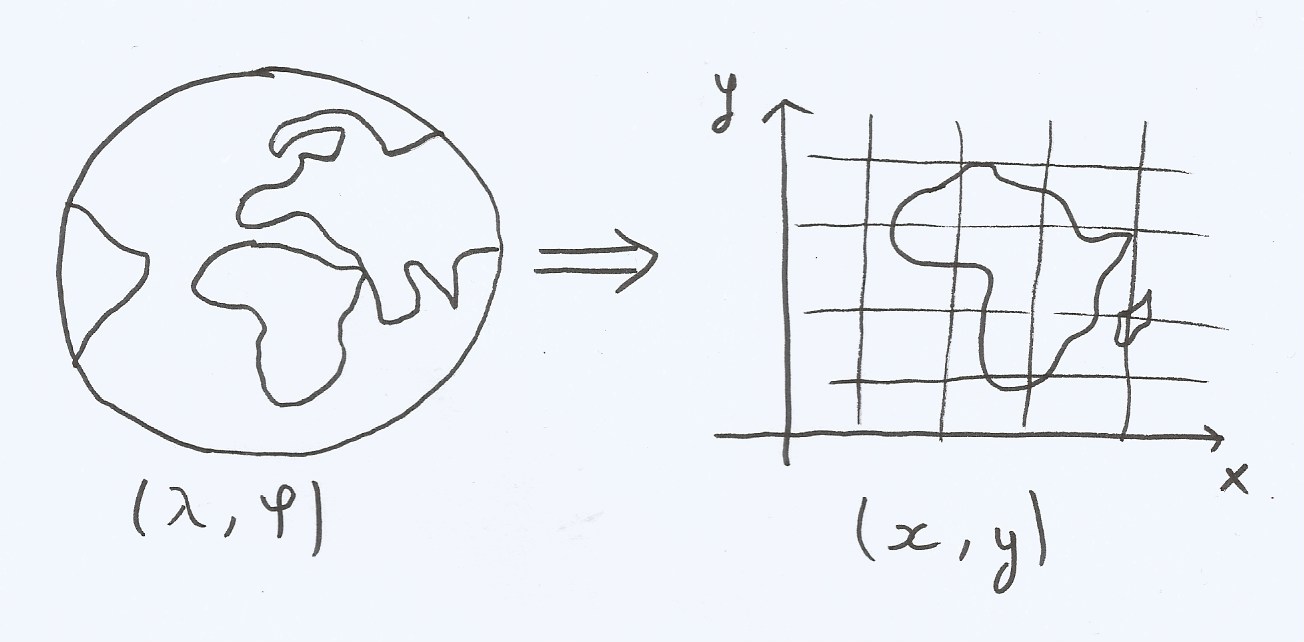
Malheureusement, aucune de ces solutions ne permet de représenter la surface de la Terre dans le plan sans distorsion sur les propriétés suivantes:

• aire
• angle
• distance
• relèvement
• échelle

Une projection pourra cependant être construite pour préserver une ou plusieurs de ces propriétés, au détriment des autres. On en distingue plusieurs types:

• projection équivalente: conserve les surfaces
• projection conforme: conserve les angles, donc les formes
• projection équidistance: conserve les distances

Les différents systèmes de projection font l’objet d’une classification. Le site https://spatialreference.org/ permet de référencer la plupart des projections existantes.

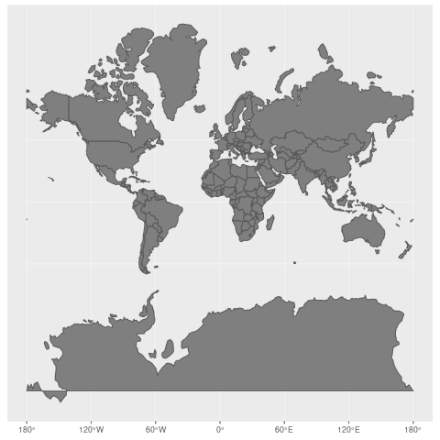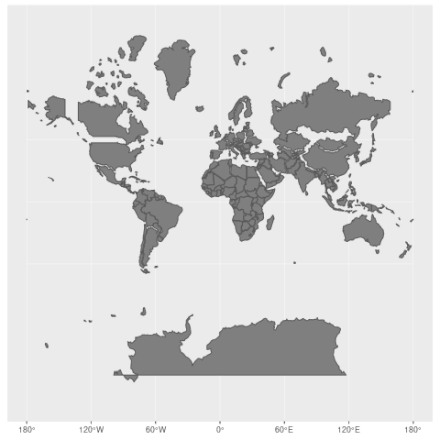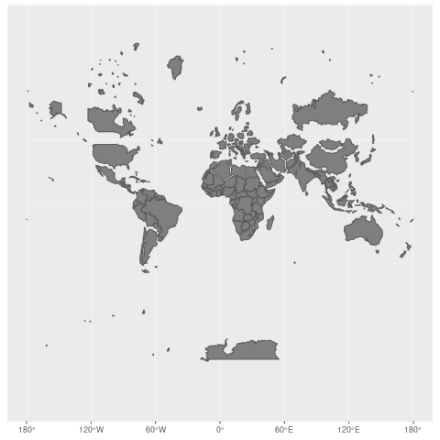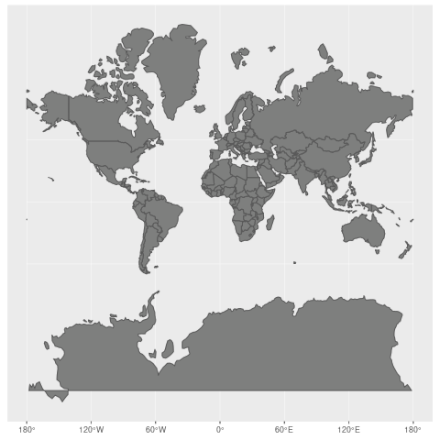
Une projection bien connue est la projection Web Mercator (EPSG:3857) qui est utilisée par la plupart des sites de cartographie en ligne, parmi lesquels Google Maps, OpenStreetMaps, Mapbox, Bing Maps et bien d’autres.

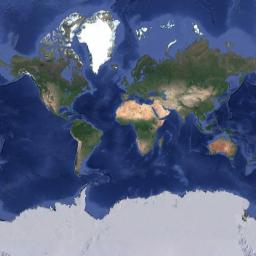
Cette projection conserve les angles mais distord les aires près des pôles: